Last time I wrote up the basics of a tip sent in by Evan over at Agile Geoscience. This technology is very neat, if you haven't read that post first, please do and watch the TED talk. This post is going to be about how we could apply this to problems in geoscience. Some of these ideas are "low hanging fruit" that could be relatively easy to accomplish, others are in need of a few more PhD students to flesh them out. I'd love to work on it myself, but I keep hearing about this thing called graduation and think it sounds like a grand time. Maybe after graduation I can play with some of these in detail, maybe before I can just experiment around a bit.
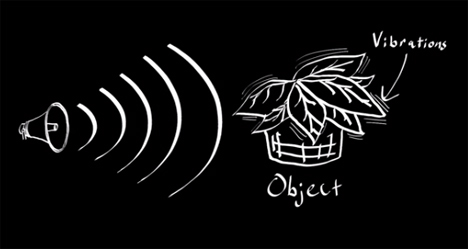
In his email to me, Evan pointed out that this visual microphone work IS seismology of sorts. In seismology we look at the motion of the Earth with seismometers or geophones. If we have a lot of them and can look at the motion of the Earth in a lot of places over time, we can learn a lot about what it's like inside the Earth. This type of survey has been used to understand problems as big as the structure of the Earth and as small as finding artifacts or oil in shallow deposits. In (very) general terms we look at very low frequency waves for Earth structure problems with periods of a second to a few hundred seconds. For more near surface problems we may look at signals up to a few hundred cycles per second (Hz). Remember in the last post I said that we collect audio data at around 44,200 Hz? That's because as humans we are able to hear up to around 20,000 Hz. All of this is a lot higher frequency than we ever use in geoscience... I'm thinking that makes this technique somewhat easier to apply and maybe even able to use poor quality images.
So what could it be used for? Below are a few bullet points of ideas. Please add to them in the comments or tear them apart. I agree with Evan that there is some great potential here.
- Find/visualize/simulate stress and strain concentration in heterogeneous materials.
- Extract modulus of rock from video of compression tests. Could be as simple as stepping on the rock.
- Extend the model to add predicted failure and show expected strain right before failure.
- Look at a sample from multiple camera views and combine for the full anisotropic properties. This smells of some modification of structure from motion techniques.
- Characterize complicated machines stiffness/strain to correct for it when reducing experimental data without complex models for the machine.
- Try prediction of building response during shaking.
- What about perturbing bodies of water and modeling the wave-field?
With everything in science, engineering, and life, there are tradeoffs. What are the catches here? Well, the resolution is pretty good, but may not be good enough for the small differences in properties we sometimes deal with. In translating this over to work on seismic data I think a lot of algorithm changes would have to happen that may end up making it about the same utility as our first-principles approaches. A big limitation for earthquake science is what happens at large strains. The model looks at small strains/vibrations to model linear elastic behavior. That's like stretching a spring and letting it spring back (remember Hooke's Law?). Things get interesting in the non-linear part of deformation when we permanently deform things. Imagine that you stretch the spring above much further than it was designed to be. The nice linear-elastic behavior would go away and plastic deformation would start. You'd deform the spring and it wouldn't ever spring back the same way it was again. Eventually, as you keep stretching, the spring would break. The non-linear parts of deformation are really important to us in earthquake science for obvious reasons. For active seismic survey people, the small strain approximation isn't bad though.
Another issue I can imagine is combining video from different orientations to recover the full behavior of the material. I don't know all of the details of Abe's algorithm, but I think it would have problems with anisotropic materials. Those are materials that behave differently in different directions. Imagine a cube that can be easily squeezed on two opposing faces, but not easily squeezed on the others. Some rocks behave in such a way (layered rocks in particular). That's really important since they are also common rocks for hydrocarbon operations to target! Surrounding the sample area with different views (video or seismic) and using all of that information should do the job, but it's bound to be pretty tricky.
The last thing that strikes me is processing time. I don't think I've seen any quotes of how long the processing of the video clips took to recover the audio. While I don't think it's ludicrous, I think the short clips could conceivably take a few hours per every 10 seconds (this is a guess). For large or long duration geo experiments that could become an issue.
So what's the end story? Well, I think this is a technology that we haven't seen the last of. The techniques are only going to get better and processors faster to let us do more number crunching. I'm curious to watch this develop and try to apply it in some basic experiments and see what happens. What would you try this technique on? Leave it in the comments!